🧭 1. Introdução: o que é o SAC e por que ele cai tanto em concurso público
Quando alguém faz um financiamento, principalmente de imóvel, logo surge aquele palavrão no contrato: “Sistema de Amortização SAC”.
A maioria das pessoas assina sem pensar muito no que isso significa — mas quem estuda para concurso precisa entender.
Esse sistema é um dos queridinhos das bancas, e não é à toa: ele aparece direto em provas que cobram Matemática Financeira, como as do Banco do Brasil, Caixa, SEFAZ, Polícia Federal e diversos concursos de tribunais.
Mas afinal, o que o SAC tem de tão especial? 🤔
👉 Para mais aulas sobre MATEMÁTICA FINANCEIRA, confira nossa seção dedicada ao tema!
💬 O que o SAC realmente faz
De forma simples, o SAC (Sistema de Amortização Constante) é um modelo de pagamento usado quando você faz um empréstimo ou financiamento.
Ele serve para organizar o jeito como você devolve o dinheiro que pegou emprestado.
A lógica é assim:
- parte do valor pago em cada parcela é amortização (a devolução do valor principal);
- e o resto é juros, calculado sobre o saldo que ainda falta pagar.
A diferença é que, no SAC, a amortização é sempre igual — constante mesmo.
Como os juros vão diminuindo com o tempo (porque o saldo devedor fica menor a cada pagamento), as parcelas também diminuem.
Ou seja:
💸 as primeiras parcelas são mais altas,
mas com o passar do tempo o peso vai ficando cada vez mais leve.
📊 Um exemplo rápido
Imagine um financiamento de R$ 10.000,00 para pagar em 5 parcelas anuais, pelo sistema SAC.
A amortização será constante: R$ 2.000,00 por ano (10.000 ÷ 5).
Os juros, no entanto, são calculados sobre o valor que ainda falta quitar.
No começo, você deve mais — então os juros são maiores.
Depois, o saldo vai diminuindo e os juros também.
Por isso:
- 1ª parcela: amortização + juros sobre 10.000
- 2ª parcela: amortização + juros sobre 8.000
- 3ª parcela: amortização + juros sobre 6.000
… e assim até quitar tudo.
O resultado?
As prestações vão caindo com o tempo — e é justamente isso que as bancas querem que você perceba nas questões.
🎯 Por que o SAC cai tanto em concurso público
Porque ele junta conceito e cálculo.
É um tema perfeito para testar se o candidato sabe interpretar tabelas, identificar padrões e entender juros compostos na prática.
E o mais curioso: apesar de parecer complicado, o SAC é super lógico.
Quem entende a ideia de “amortização constante” e “juros sobre o saldo devedor” consegue resolver 90% das questões sem precisar decorar fórmulas.
💡 O que você vai ver neste artigo
Neste conteúdo, a gente vai:
- entender o que é amortização de verdade (sem enrolação);
- ver como o SAC funciona na prática;
- montar uma tabela passo a passo;
- e resolver duas questões de concurso comentadas, mostrando o raciocínio por trás de cada uma.
A ideia é que, quando você chegar ao final, consiga bater o olho numa questão e pensar:
👉 “Ah, é SAC — amortização constante e parcelas decrescentes!”
Simples assim.
🚀 Dica rápida para já começar acertando
Se no enunciado aparecer algo como
“as parcelas diminuem ao longo do tempo”
ou
“a amortização é constante”
… pode apostar: é SAC.
Anote isso — é um dos atalhos mais valiosos pra quem quer garantir ponto fácil na prova.
🧩 2. Conceito básico de amortização
Antes de mergulhar nas fórmulas e tabelas do Sistema de Amortização SAC, a gente precisa entender o que significa, afinal, amortizar.
Essa palavrinha aparece tanto em contratos de banco quanto nas provas, mas pouca gente realmente sabe o que ela quer dizer. Então, bora simplificar 👇
💬 O que é amortização
Amortizar nada mais é do que pagar uma parte da dívida principal — aquele dinheiro que você pegou emprestado.
Não estamos falando dos juros, e sim da dívida em si, do valor que efetivamente precisa ser devolvido.
Pensa assim:
Se você pega R$ 10.000,00 emprestados, esse valor é o principal.
Cada vez que você paga uma parcela, uma parte dela vai para os juros (o “aluguel” do dinheiro) e outra parte vai para amortizar — ou seja, diminuir o saldo devedor.
Então:
Amortizar é diminuir a dívida.
Simples assim.
🧮 Componentes de uma prestação
Quando você paga uma prestação de empréstimo, ela sempre tem duas partes principais:
| Parte da parcela | O que é | Explicação rápida |
| Amortização | É o valor que reduz o saldo devedor | Você devolve parte do que pegou emprestado |
| Juros | É o custo do dinheiro | O banco cobra sobre o que ainda falta pagar |
Assim:
Prestação = Amortização + Juros
Essa fórmula é o coração de qualquer sistema de amortização — seja SAC, Price ou misto.
O que muda entre eles é como essas duas partes se comportam ao longo do tempo.
📉 No SAC, a amortização é constante
O nome SAC vem de Sistema de Amortização Constante, e isso já entrega o segredo:
- a amortização é igual em todas as parcelas;
- os juros diminuem com o tempo;
- e, por consequência, as parcelas (prestações) vão caindo.
💡 Dica visual:
Imagine uma escada invertida.
A amortização é o degrau fixo — sempre igual.
Os juros vão diminuindo, então o valor total (prestação) desce degrau por degrau até o final do contrato.
📘 Exemplo simples para entender o conceito
Vamos supor um empréstimo de R$ 12.000,00, dividido em 4 parcelas anuais, com juros de 10% ao ano, no sistema SAC.
1️⃣ Cálculo da amortização:

Ou seja, em cada parcela, o cliente vai amortizar R$ 3.000,00.
2️⃣ Cálculo dos juros:
Os juros incidem sobre o saldo devedor.
Assim:
- 1ª parcela → juros sobre 12.000
- 2ª parcela → juros sobre 9.000
- 3ª parcela → juros sobre 6.000
- 4ª parcela → juros sobre 3.000
3️⃣ Cálculo das prestações:
| Parcela | Saldo Devedor Inicial | Juros (10%) | Amortização | Prestação Total |
| 1ª | 12.000 | 1.200 | 3.000 | 4.200 |
| 2ª | 9.000 | 900 | 3.000 | 3.900 |
| 3ª | 6.000 | 600 | 3.000 | 3.600 |
| 4ª | 3.000 | 300 | 3.000 | 3.300 |
Note como as prestações diminuem a cada período, mas a amortização é constante.
É isso que caracteriza o SAC!
🧠 Interpretação prática
No início, o valor da prestação é mais pesado, porque os juros sobre o saldo devedor ainda são altos.
Mas a vantagem é que, ao longo do tempo, a dívida cai rapidamente — o que significa que o total de juros pagos é menor do que no Sistema Price, por exemplo.
Por isso, o SAC costuma ser preferido em financiamentos longos, como os imobiliários, onde o objetivo é pagar menos juros no total.
⚖️ SAC x Price (visão rápida)
| Característica | SAC | Price (Tabela Price) |
| Amortização | Constante | Crescente |
| Juros | Decrescentes | Decrescentes |
| Prestação | Decrescente | Constante |
| Total de juros pagos | Menor | Maior |
| Primeiras parcelas | Mais altas | Mais baixas |
⚙️ 3. Como funciona o Sistema de Amortização SAC
Agora que você já entendeu o que é amortização, vamos ver como o Sistema de Amortização Constante (SAC) realmente funciona na prática.
Essa é a parte em que a mágica acontece — onde você aprende a montar a tabela, entender como os juros caem e perceber por que as parcelas diminuem com o tempo.
🧩 A ideia central do SAC
O SAC é um sistema em que a amortização do principal é sempre igual.
Isso quer dizer que, em cada período (mês, trimestre, ano etc.), o valor que reduz o saldo devedor é o mesmo.
O que muda são os juros — que vão sendo calculados sobre o saldo devedor restante.
Como esse saldo vai caindo, os juros caem também. Resultado:
👉 as parcelas começam altas e vão diminuindo gradativamente.
🧮 Fórmulas básicas do SAC
Você não precisa decorar fórmulas complicadas para mandar bem em prova.
Mas existem duas continhas simples que valem ouro:
1️⃣ Amortização constante:
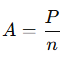
Onde:
- A = valor da amortização em cada parcela
- P = valor total do empréstimo
- n = número de parcelas
2️⃣ Juros de cada período:
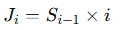
Onde:
- JI = juros da parcela i
- Si−1 = saldo devedor antes do pagamento da parcela
- i = taxa de juros do período
3️⃣ Prestação (ou parcela total):
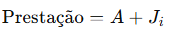
Simples assim.
💡 Exemplo prático — Montando a tabela passo a passo
Vamos montar juntos uma tabela SAC com números fáceis de entender, como os que costumam aparecer nas provas.
Situação:
Um empréstimo de R$ 20.000,00 será pago em 4 parcelas mensais, com juros de 5% ao mês, no sistema SAC.
🧾 Passo 1: Calcular a amortização
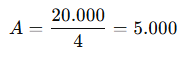
👉 Amortização constante de R$ 5.000,00 por mês.
🧾 Passo 2: Calcular os juros e prestações de cada parcela
| Parcela | Saldo Devedor Inicial | Juros (5%) | Amortização | Prestação | Saldo Final |
| 1ª | 20.000 | 1.000 | 5.000 | 6.000 | 15.000 |
| 2ª | 15.000 | 750 | 5.000 | 5.750 | 10.000 |
| 3ª | 10.000 | 500 | 5.000 | 5.500 | 5.000 |
| 4ª | 5.000 | 250 | 5.000 | 5.250 | 0 |
📊 Interpretação da tabela
Observe o padrão:
- A amortização (R$ 5.000) é igual em todas as parcelas.
- Os juros caem (1.000 → 750 → 500 → 250).
- E, por isso, as prestações diminuem (6.000 → 5.750 → 5.500 → 5.250).
Esse comportamento é a marca registrada do SAC.
A dívida vai sendo reduzida mais rapidamente, e o total pago de juros, no fim das contas, é menor do que em outros sistemas, como o Price.
🔍 Dica de prova
Muitas questões de concurso não pedem a tabela inteira, mas sim algo como:
“Determine o valor da 3ª prestação”
ou
“Calcule os juros pagos na segunda parcela”.
Então, o segredo é identificar o padrão:
- amortização é constante;
- saldo devedor diminui em progressão aritmética (mesmo valor a cada passo);
- juros caem proporcionalmente.
Com isso, dá pra resolver em 2 ou 3 linhas, sem precisar montar tudo.
🧠 Exemplo rápido de raciocínio de prova
Questão-treino:
Um empréstimo de R$ 12.000,00 será pago em 3 parcelas iguais, pelo sistema SAC, com taxa de 10% ao mês.
Qual o valor da segunda prestação?
Resolução:
1️⃣ Amortização:
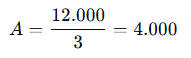
2️⃣ Juros da 2ª parcela → saldo devedor antes dela é 8.000 (pois já foi amortizado 4.000 na primeira).
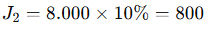
3️⃣ Prestação:
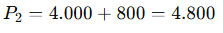
✅ Resposta: R$ 4.800,00
Pronto. Sem fórmulas complicadas, só raciocínio lógico.
💬 Comparando com a vida real
Se você já fez um financiamento imobiliário, provavelmente já viu o SAC em ação.
Nos primeiros boletos, as parcelas são maiores; depois, com o tempo, o valor começa a cair.
Isso acontece justamente porque a amortização é fixa e os juros diminuem conforme o saldo é reduzido.
📘 Resumindo a lógica do SAC
| Elemento | Comportamento |
| Amortização | Constante |
| Juros | Decrescentes |
| Prestação | Decrescente |
| Saldo devedor | Diminui linearmente |
| Total de juros pagos | Menor do que no Price |
Exercício de Concurso Público Resolvido
📄 Enunciado
Um servidor público contraiu um empréstimo de R$ 30.000,00 para pagar em 3 parcelas mensais e consecutivas, com juros de 10% ao mês, pelo Sistema de Amortização Constante (SAC).
Com base nessas informações, determine o valor da segunda prestação.
🧠 Passo 1 — Identificar o tipo de sistema
A questão já diz que é SAC, então gravamos:
- Amortização constante
- Prestação decrescente
- Juros calculados sobre o saldo devedor
Nada de tentar aplicar fórmula de Price aqui — o segredo é a lógica.
🧮 Passo 2 — Calcular a amortização
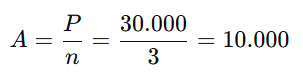
👉 Cada parcela vai amortizar R$ 10.000,00.
Isso significa que, a cada pagamento, o saldo devedor diminui em 10 mil.
📉 Passo 3 — Calcular os juros
A taxa é 10% ao mês, e os juros são sempre calculados sobre o saldo devedor antes do pagamento.
| Parcela | Saldo Devedor Antes | Juros (10%) |
| 1ª | 30.000 | 3.000 |
| 2ª | 20.000 | 2.000 |
| 3ª | 10.000 | 1.000 |
💰 Passo 4 — Calcular o valor das prestações
Lembrando:
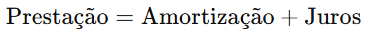
| Parcela | Amortização | Juros | Prestação | Saldo Final |
| 1ª | 10.000 | 3.000 | 13.000 | 20.000 |
| 2ª | 10.000 | 2.000 | 12.000 | 10.000 |
| 3ª | 10.000 | 1.000 | 11.000 | 0 |
✅ Resposta: Segunda prestação = R$ 12.000,00
🧩 Passo 5 — Interpretação e raciocínio de prova
Repare como as parcelas diminuem de forma linear:
13.000 → 12.000 → 11.000.
Isso acontece porque a amortização é constante (10.000) e os juros caem 1.000 a cada período.
É um comportamento típico do SAC, e as bancas adoram explorar esse padrão.
Na prática, se o candidato entende essa lógica, ele consegue resolver qualquer questão do tipo em 30 segundos — sem montar tabela completa.
Por exemplo:
- Se a primeira prestação é 13.000 e a amortização é constante (10.000), basta perceber que o juro da segunda é 2.000 → pronto, prestação = 12.000.
⚡ Dica de ouro (que já caiu em prova da Cesgranrio)
Quando o enunciado mencionar “parcelas decrescentes” e “amortização constante”, é SAC, sem dúvida.
E o comportamento dos valores sempre será em progressão aritmética decrescente, com diferença igual à queda dos juros.
Ou seja:
A diferença entre as parcelas é igual à diferença entre os juros sucessivos.
No exemplo acima:
13.000 → 12.000 → 11.000 → diferença de 1.000 = diferença entre os juros (3.000, 2.000, 1.000).
💬 Conclusão do exercício
👉 O SAC é previsível: basta saber o valor da amortização e a taxa de juros para determinar qualquer parcela.
A Cesgranrio costuma colocar números redondos justamente pra testar entendimento, não cálculo pesado.
No seu rascunho, sempre pense assim:
“Saldo devedor → calcula juros → soma com amortização → pronto, achei a prestação.”
Simples, rápido e certeiro. 🎯
👉 Curtiu o conteúdo até aqui? Então não pare agora! 👉 Clique aqui e confira mais exercícios resolvidos do Sistema SAC para fixar de vez o assunto!
Resumo prático e comparativo: SAC x Price
Agora que você já entendeu o SAC, é hora de fazer aquele resumão de bolso pra nunca mais confundir com o Sistema Price (também chamado de Sistema Francês de Amortização).
A maioria dos alunos erra nas provas porque mistura os dois — então, bora deixar tudo claro 👇
| 💡 Característica | 🧱 SAC (Amortização Constante) | 📈 Price (Amortização Crescente) |
| Valor da Amortização | Igual em todas as parcelas | Aumenta ao longo do tempo |
| Valor dos Juros | Diminui a cada parcela | Diminui, mas de forma mais lenta |
| Valor da Prestação | Decrescente | Constante |
| Cálculo da Prestação | Amortização + Juros | Fórmula de prestação fixa (com fator de juros) |
| Custo total | Mais barato ao final | Mais caro (por manter juros maiores por mais tempo) |
| Indicado para | Quem quer pagar menos juros e pode começar com parcelas maiores | Quem quer parcelas fixas (previsibilidade no orçamento) |
| Mais cobrado em concurso | SAC (geralmente com cálculo de parcelas e juros totais) | Price (em questões conceituais e comparação) |
📚 Exemplos de pegadinhas que caem nas provas
- “No SAC, as parcelas são iguais” → ❌ Errado!
No SAC, as parcelas são decrescentes, porque os juros caem a cada período. - “O sistema Price é o mais barato” → ❌ Errado também!
Ele é mais caro no total, pois você paga mais juros ao longo do tempo. - “No SAC, a amortização é constante e os juros diminuem” → ✅ Perfeito!
🔍 Dica visual rápida (pra gravar na mente)
- SAC = escadinha pra baixo 🪜
→ Parcelas começam altas e vão diminuindo. - Price = linha reta ➖
→ Parcelas sempre iguais do início ao fim.
💬 Em resumo
👉 No SAC, o alívio vem rápido — as parcelas caem e o saldo devedor diminui mais depressa.
👉 No Price, a tranquilidade vem na regularidade — você paga o mesmo valor todo mês, mas desembolsa mais juros no total.
Saber essas diferenças é meio caminho andado pra acertar qualquer questão sobre amortização em concurso.
E o melhor: muitas vezes o enunciado não pede cálculo, só quer saber quem é quem.
🎯 Conclusão: Dicas para prova e vida real
Chegamos ao fim do nosso guia, mas agora vem a parte mais importante: como usar isso com estratégia — tanto nas provas quanto fora delas.
🧠 1. Dicas para gabaritar nas provas
💥 1. Memorize a essência, não fórmulas.
As bancas (FCC, Cesgranrio, FGV) amam testar o entendimento do comportamento das parcelas — não apenas contas.
Exemplo clássico:
“No SAC, as parcelas são crescentes, decrescentes ou constantes?”
➡️ Resposta: Decrescentes, sempre.
💥 2. Monte uma mini-tabela mental.
Se o exercício der 3 ou 4 parcelas, calcule a primeira e a última — e observe o padrão.
Isso evita erros e economiza tempo.
💥 3. Leia com calma o que o problema quer.
Nem sempre ele pede a prestação!
Às vezes, quer o total de juros, o saldo devedor após uma parcela ou até a diferença entre prestações.
💥 4. SAC e Price caem juntos.
Prepare-se pra comparar: “Qual sistema tem parcelas constantes?” / “Qual paga mais juros?”.
Essas são perguntas certeiras em provas de bancos, tribunais e áreas administrativas.
💰 2. Dicas pra vida real
Mesmo fora dos concursos, entender amortização faz diferença.
Sabe aquele financiamento de carro, casa ou empréstimo pessoal?
Pois é — tudo isso usa Price ou SAC.
💡 Exemplo prático:
- SAC: você paga mais no início, mas quita mais rápido e economiza juros.
- Price: parcelas fixas e previsíveis, mas o banco lucra mais com você.
Se o seu objetivo é pagar menos juros, o SAC é seu melhor amigo.
Se você quer parcelas iguais pra organizar o orçamento, o Price é mais confortável.
🧩 3. Dica bônus: entenda o “padrão de decrescimento”
A diferença entre as parcelas no SAC é sempre igual à diferença entre os juros sucessivos.
Então, se o juro cai R$ 500 de uma parcela pra outra, as prestações também caem R$ 500.
Essa lógica é a chave de ouro pra resolver rápido sem precisar montar tudo no papel.
🚀 4. Fechando com uma reflexão
Saber matemática financeira em concurso não é só pra acertar questão — é pra entender como o dinheiro funciona.
Quem domina SAC e Price entende juros, tempo e planejamento — e isso vale tanto pra prova quanto pra vida.
🎓 Resumo final:
- SAC = amortização constante, parcelas decrescentes.
- Price = amortização variável, parcelas fixas.
- SAC = menor custo total.
- Price = mais previsível, mas mais caro.
🏁 Conclusão geral
Se o examinador quiser te confundir, ele vai usar termos parecidos e tabelas com valores próximos.
Mas se você lembrar da essência — amortização constante e parcelas decrescentes no SAC — já garantiu o ponto.
📘 Então, na hora da prova:
- Respire,
- Veja o sistema que está sendo usado,
- Pense no comportamento das parcelas,
- E resolva com confiança.
Você não está apenas estudando pra passar — está entendendo o que move o sistema financeiro. 💪
🎯 Missão concluída? Quase!
Se você chegou até aqui, já deu um grande passo para dominar o Sistema SAC.
Mas para realmente gabaritar as provas de concurso público, é essencial praticar!
👉 Acesse agora o Banco de Questões e veja como esse tema cai nas provas!






















