Se você está se preparando para concursos públicos no Brasil, certamente já se deparou com questões de Análise Combinatória – especialmente sobre arranjos. Esse tema é frequente em provas de matemática e raciocínio lógico, e dominá-lo pode garantir pontos preciosos!
Neste artigo, vamos explicar de forma clara e direta o que são arranjos simples e arranjos com repetição, mostrando a diferença entre eles e como calcular cada um. Além disso, traremos exemplos práticos que caem em concursos, como formação de senhas, placas de veículos e códigos numéricos.
Se você quer evitar erros e resolver essas questões com confiança, continue lendo – esse conteúdo foi feito para ajudar você a mandar bem na prova!
Arranjos simples
Os arranjos simples são uma maneira de organizar elementos de um conjunto, levando em conta a ordem deles e sem repetir nenhum. Imagine que você tem um grupo com n elementos e quer formar grupos menores com p elementos de cada vez. Se a ordem em que esses elementos aparecem faz diferença, então você está lidando com um arranjo simples.
Uma dúvida comum é: qual a diferença entre arranjo e combinação? A resposta é simples — nos arranjos, a ordem dos elementos importa, enquanto nas combinações, não importa.
Para calcular quantos arranjos diferentes podemos formar, usamos a seguinte fórmula:
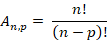
Em que:
- An,p é o arranjo de n elementos tomados de p em p
- n é quantidade de elementos
- p é a quantidade de elementos por agrupamentos
Essa fórmula ajuda a descobrir todas as possíveis formas de organizar p elementos de um total de n, sem repetir e respeitando a ordem. É um conceito muito usado em matemática, lógica e provas de concursos, então vale a pena entender bem!
O Que é um Número Fatorial e Como Calcular com um Exemplo Simples
Um número fatorial representa o produto de todos os números inteiros positivos de 1 até um determinado número natural n, sendo indicado pelo símbolo n!
Esse conceito é fundamental em áreas como matemática, estatística e programação, sendo amplamente utilizado em cálculos de permutações e combinações.
Por exemplo, o fatorial de 4 é calculado como 4! = 4 × 3 × 2 × 1 = 24. Entender o que é um número fatorial é essencial para quem deseja dominar tópicos de matemática básica e avançada.
Exemplos de Exercícios Resolvidos de Arranjo Simples para Estudar
Exemplo 1: Arranjos Simples com Letras
Problema:
Quantos arranjos simples de 2 letras podemos formar com as letras A, B e C?
Passo 1 – Identificar os elementos:
Temos 3 letras: A, B, C → então, n = 3
Queremos formar grupos com 2 letras → então, p = 2
Passo 2 – Usar a fórmula do arranjo simples:
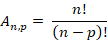
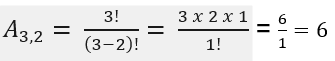
Resposta: Existem 6 arranjos simples de 2 letras com o conjunto A, B, C.
Exemplo 2: Senhas com Dígitos Diferentes
Problema:
Quantas senhas de 3 dígitos diferentes podemos formar com os números 1, 2, 3, 4?
Passo 1 – Identificar os dados do problema:
Temos 4 dígitos: 1, 2, 3, 4 → então, n = 4
Vamos formar senhas com 3 dígitos → então, p = 3
Passo 2 – Aplicar a fórmula do arranjo simples:
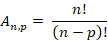
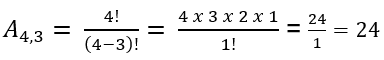
Resposta: Podemos formar 24 senhas diferentes de 3 dígitos com os números 1, 2, 3 e 4, sem repetições e com ordem.
Arranjos com Elementos Repetidos
O arranjo com repetição é um tipo de agrupamento em que a ordem dos elementos importa e é permitido repetir os itens. Ou seja, se você pode usar o mesmo número ou letra mais de uma vez, como em uma senha “112” ou “AAA”, está usando esse tipo de arranjo.
Esse conceito é muito comum em situações do dia a dia, como:
- Criar senhas numéricas ou alfanuméricas;
- Montar placas de veículos;
- Combinar cores, códigos ou objetos repetíveis.
Para resolver esse tipo de problema, usamos uma fórmula específica para o arranjo com repetição — que é diferente da usada no arranjo simples, onde não há repetição. Por isso, é fundamental saber diferenciar as situações, para usar a técnica de contagem correta.
A fórmula para calcular o número total de arranjos com repetição é bem direta e fácil de aplicar. Com ela, conseguimos saber rapidamente quantas combinações possíveis podem ser feitas quando os elementos podem se repetir.

Em que :
- An,p é o arranjo de n elementos tomados de p em p
- n é quantidade de elementos
- p é a quantidade de elementos que serão escolhidos
Exemplos de Exercícios Resolvidos de Arranjo com Repetição para Estudar
Exemplo 1: Criação de Senhas Numéricas com Repetição
Problema:
Quantas senhas de 4 dígitos podemos formar usando os números de 0 a 9, permitindo repetir os dígitos?
Passo 1 – Identificar os dados:
- Temos 10 dígitos disponíveis: 0, 1, 2, …, 9 → então n = 10
- A senha terá 4 dígitos → então p = 4
Passo 2 – Verificar se há repetição:
Sim, podemos repetir os números (por exemplo: 1111 ou 2020).
Passo 3 – Aplicar a fórmula do arranjo com repetição:

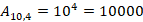
📌 Importante: Aqui a ordem importa — a senha 1234 é diferente de 4321.
Logo, existem 10.000 combinações possíveis de senhas de 4 dígitos quando a repetição é permitida.
Exemplo 2: Combinação de Placas de Carros (Modelo Antigo do Brasil)
Problema:
Quantas placas de carro podem ser formadas no formato antigo brasileiro: 3 letras seguidas por 4 números (ex: ABC-1234), permitindo repetir letras e números?
Passo 1 – Identificar os dados:
- Letras disponíveis no alfabeto: 26 → n₁ = 26 (para letras)
- Dígitos disponíveis: 10 → n₂ = 10 (para números)
- Queremos formar uma placa com 3 letras e 4 números
Passo 2 – Usar a fórmula para cada parte:
Como há repetição permitida em ambos os casos, usamos a fórmula do arranjo com repetição:

Parte das letras
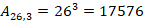
Parte dos números

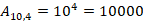
Passo 3 – Multiplicar os dois resultados:
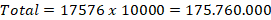
Resposta: Podemos formar 175.760.000 placas diferentes no modelo antigo, com 3 letras e 4 números, permitindo repetição.
Agora que você já entendeu a diferença entre arranjos simples (ordem importa, sem repetição) e arranjos com repetição (ordem importa, com repetição), ficou muito mais fácil resolver questões de concursos que envolvem contagem e combinações.
Esse conhecimento é essencial para:
✔ Provas de matemática básica e raciocínio lógico (como ENEM, concursos bancários e tribunais).
✔ Cálculo de senhas, placas e códigos (muito comum em questões de lógica).
✔ Evitar pegadinhas (muitos candidatos erram por confundir arranjos com combinações).
Dica extra: Pratique com os exemplos resolvidos e tente criar variações para fixar o conteúdo. Se este artigo ajudou você, compartilhe com outros concurseiros – quanto mais gente bem preparada, melhor!
Bons estudos e sucesso na sua jornada de concursos! 🚀
“Quer praticar com questões sobre o Princípio Fundamental da Contagem? Acesse aqui e resolva exercícios para reforçar seus estudos!”
Dica de Livro para otimizar o seu estudo
Se você procura um material claro e direto para aprender matemática voltada para concursos, esse livro é uma ótima escolha. Com explicações simples, exercícios resolvidos e acesso a videoaulas, ele é ideal para quem quer dominar o conteúdo com praticidade. Confira na Amazon.





















