Este material apresenta exercícios resolvidos sobre Progressão Aritmética (PA), abordando conceitos como termo geral, razão e soma dos termos. Com explicações detalhadas e passo a passo, o conteúdo é ideal para estudantes que desejam reforçar seus conhecimentos em sequências numéricas e suas aplicações.
Sugestão:
Caso precise revisar os conceitos básicos de PA, acesse a sessão dedicada a Progressão Aritmética no site. Lá você encontrará explicações detalhadas, exemplos e exercícios adicionais para reforçar seu aprendizado.
EXERCÍCIOS:
1 – (FCC) – Uma sequência numérica é formada por números que seguem uma progressão aritmética. Sabendo que o 5º termo é 18 e o 10º termo é 33, qual é a razão dessa PA?
a) 2
b) 3
c) 4
d) 5
e) 6
RESOLUÇÃO:
Dados:
- O 5º termo (a5) é 18.
- O 10º termo (a10) é 33.
Fórmula do termo geral de uma PA:
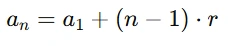
onde:
- an é o n-ésimo termo,
- a1 é o primeiro termo,
- r é a razão da PA.
Aplicando para o 5º termo:
a5 = a1 + 4r = 18 (1)
Aplicando para o 10º termo:
a10 = a1 + 9r = 33 (2)
Subtraindo a equação (1) da equação (2):
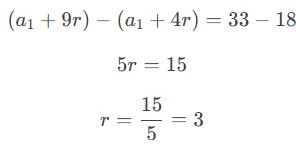
✅ Resposta: b) 3
2 – (VUNESP) – Em uma PA, o 1º termo é 8 e a razão é 3. Qual é o 25º termo?
a) 83
b) 80
c) 81
d) 75
e) 78
RESOLUÇÃO:
Para encontrar o 25º termo de uma Progressão Aritmética (PA), utilizamos a fórmula do termo geral:
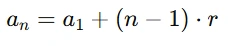
Onde:
- an é o termo que queremos encontrar (25º termo),
- a1 é o primeiro termo (8),
- r é a razão (3),
- n é a posição do termo (25).
Substituindo os valores na fórmula:
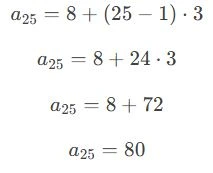
✅ Resposta: b) 80
3 – (CESGRANRIO – Adaptada) – A soma dos 20 primeiros termos de uma progressão aritmética (PA) é 710. Sabendo que o primeiro termo é 5, determine o último termo dessa progressão.
a) 60
b) 62
c) 64
d) 66
e) 68
RESOLUÇÃO:
Dados:
- Soma dos 20 primeiros termos (S20) = 710.
- Primeiro termo (a1) = 5.
- Queremos encontrar o último termo (a20).
Fórmula da soma dos n primeiros termos de uma PA:
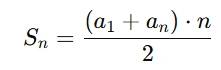
Aplicando para n = 20:
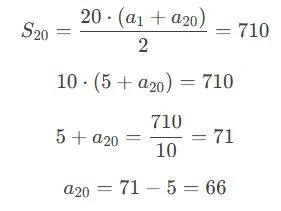
Portanto, o último termo (a20) é 66.
✅ Resposta: d) 66
4 – (IBFC) – O 3º termo de uma PA é 10, e o 7º termo é 26. Qual é a soma dos 10 primeiros termos dessa progressão?
a) 175
b) 180
c) 185
d) 190
e) 200
A fórmula do n-ésimo termo de uma PA é:
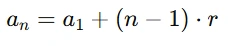
Onde:
- an é o termo de posição n
- a1 é o primeiro termo
- r é a razão da PA
Sabemos que:
- O 3º termo é 10 → a3 = 10
- O 7º termo é 26 → a7 = 26
Vamos aplicar a fórmula:
Para o 3º termo:
a3 = a1 +2r = 10 (1)
Para o 7º termo:
a7 = a1 + 6r = 26 (2)
Vamos subtrair a Equação 1 da Equação 2:
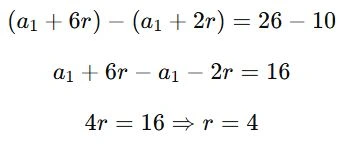
Agora substituímos r = 4 na Equação 1:
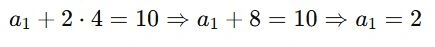
Agora usando a fórmula da soma dos n primeiros termos:
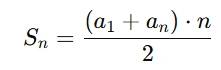
Queremos a soma dos 10 primeiros termos → n=10
Sabemos:
- a1 = 2
- Precisamos calcular o a10:
a10 = a1 + ( 10 – 1 ) ⋅ r = 2 + 9 ⋅ 4 = 2 + 36 = 38
Agora sim, podemos calcular a soma:
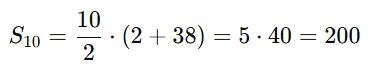
✅ Resposta: e) 200
Os exercícios resolvidos neste material demonstram a aplicação prática dos conceitos de Progressão Aritmética (PA), desde o cálculo da razão até a determinação de termos e somas. Com dedicação e prática, é possível dominar esse tema fundamental da matemática e aplicá-lo em diversos provas de concursos públicos.















