A disciplina de matemática está presente na maioria dos concursos públicos e costuma ser decisiva na pontuação dos candidatos. Entre os temas mais cobrados, o estudo de Matrizes merece atenção especial, já que gera muitas dúvidas nas provas.
👉 Dominar esse assunto pode garantir pontos preciosos na sua classificação.
Neste guia, você vai encontrar uma explicação clara e simples sobre matrizes, com definições, exemplos práticos, exercícios comentados e dicas valiosas de prova.
👉 Para mais aulas sobre MATEMÁTICA, confira nossa seção dedicada ao tema!
📍 O que é uma Matriz?
Uma matriz é uma tabela organizada em linhas e colunas, usada para armazenar números ou outros elementos.
📊 Exemplo de matriz 2×2:
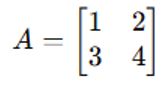
- Os números dentro da matriz são chamados de elementos.
- O índice de cada elemento mostra sua posição (linha e coluna).
- Exemplo: em A, o elemento a12 = 2 (1ª linha, 2ª coluna).
💡 Matrizes são muito utilizadas em sistemas lineares, transformações geométricas, estatística, além de serem cobradas em provas de bancos, militares e tribunais.
🔎 Tipos de Matrizes mais cobrados em Concurso Público
- Matriz Linha
- Possui apenas uma linha.
[3 7 5]
- Matriz Coluna
- Possui apenas uma coluna.

- Matriz Quadrada
- Número de linhas = número de colunas.
- Exemplo: matriz 3×3.
- Só em matrizes quadradas calculamos determinante e matriz inversa.
- Matriz Identidade (I)
- Elementos da diagonal principal = 1, demais = 0.
- Exemplo (3×3):
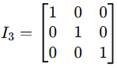
Propriedade: A ⋅ I = A
- Matriz Nula
- Todos os elementos são iguais a zero.
- Matriz Transposta (Aᵀ)
- Obtida trocando linhas por colunas.
- Exemplo:
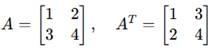
- Matriz Inversa (A-1)
- Uma matriz A terá inversa (denotada por A-1) se existir outra matriz que, ao ser multiplicada por A, resulte na matriz identidade (I).
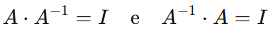
Ela só existe se o det(A) ≠ 0.
Exemplo:
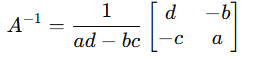
🧮 Operações com Matrizes
➕ Adição e Subtração
- Só é possível se forem do mesmo tipo (mesmo número de linhas e colunas).
- Basta somar ou subtrair os elementos correspondentes.
✖️ Multiplicação por Escalar
- Cada elemento da matriz é multiplicado por um número real.
Exemplo:
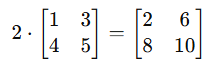
✖️ Multiplicação entre Matrizes
- Só é possível se o número de colunas da 1ª matriz = número de linhas da 2ª.
- O elemento resultante é a soma dos produtos da linha pela coluna.
⚠️ Importante: A multiplicação não é comutativa. Ou seja:
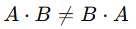
🎯 Determinantes
O determinante é um número associado a uma matriz quadrada.
📌 Regra para matriz 2×2:
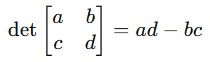
📌 Regra de Sarrus (3×3):
- Repita as duas primeiras colunas da matriz à direita.
- Some os produtos das diagonais principais.
- Subtraia os produtos das diagonais secundárias.
Exemplo:
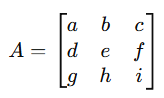
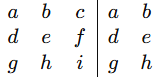
S1 = a ⋅ e ⋅ i + b ⋅ f ⋅ g + c ⋅ d ⋅ h
S2 = b ⋅ d ⋅ i + a ⋅ f ⋅ h + c ⋅ e ⋅ g
Det(A) = S1 – S2
🧩 Matriz Inversa
Para matriz 2×2:
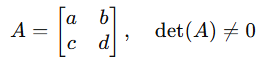
A inversa é:
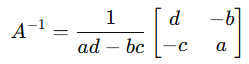
🚨 Erros Comuns em Prova
❌ Confundir multiplicação com adição.
❌ Esquecer que a multiplicação não é comutativa.
❌ Errar o sinal no determinante.
❌ Achar que toda matriz tem inversa (só se det ≠ 0).
📝 Exercícios de Concursos Anteriores Resolvidos
📌 Questão 1 (Fácil) – CESGRANRIO
Seja
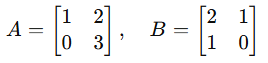
Calcule A ⋅ B
Resolução:
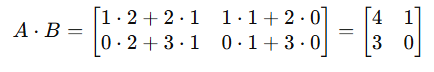
✅ Resposta Correta:
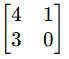
📌 Questão 2 (Médio) – FCC
Qual é o determinante da matriz:
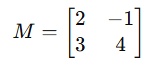
Resolução:
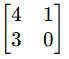
✅ Resposta Correta: 11
📌 Questão 3 (Difícil) – CESPE
Seja a matriz:
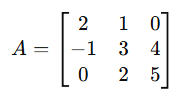
Calcule o determinante.
Resolução (Regra de Sarrus):
- Diagonais principais: 2 ⋅ 3 ⋅ 5 + 1 ⋅ 4 ⋅ 0 + 0 ⋅ (−1) ⋅ 2 = 30 + 0 + 0 = 30
- Diagonais secundárias: 0 ⋅ 3 ⋅ 0 + 2 ⋅ 4 ⋅ 2 + 1 ⋅ (−1) ⋅ 5 = 0 + 16 – 5 = 11
- det(A) = 30 – 11 = 19
✅ Resposta Correta: 19
🎓 Dicas Finais para Concurso Público
✔️ Foque em operações básicas (adição, multiplicação e determinante).
✔️ Domine a Regra de Sarrus (sempre cai em provas).
✔️ Treine cálculo de inversa (principalmente em 2×2).
✔️ Resolva muitas questões anteriores – é nelas que você vai ver o nível de cobrança real.
✅ Conclusão
O estudo de Matrizes é essencial para quem se prepara para concurso público. Apesar de parecer complicado no início, com prática você vai perceber que os cálculos seguem regras bem definidas.
👉 Resumo do que você deve dominar para a prova:
- Definições básicas e tipos de matrizes.
- Operações fundamentais.
- Determinantes (2×2 e 3×3).
- Matriz inversa (2×2).
- Propriedades principais.
🔔 Dica de ouro: Resolva todos os dias ao menos 3 exercícios de matrizes de provas anteriores. Assim, você fixa a teoria e se prepara melhor para a banca.
👉 Para mais exercícios resolvidos sobre MATRIZES, confira nossa seção exclusiva!
👉 Confira também nosso banco de questões com MAIS exercícios sobre MATRIZES E OUTROS CONTEÚDOS DE MATEMÁTICA e outros conteúdos para você treinar e aprimorar seus estudos!
👉 Continue firme nos estudos, porque a sua vaga no concurso público está cada vez mais perto!





















