Se você está se preparando para concursos públicos, já deve ter percebido que a matemática básica aparece em praticamente todas as provas.
E um dos temas que sempre cai é o famoso assunto de noções de conjuntos.
Mas pode ficar tranquilo(a)!
Neste artigo, vamos conversar sobre tudo o que você precisa saber sobre conjuntos de forma leve, descomplicada e direto ao ponto — com exemplos práticos, diagramas ilustrativos, questões resolvidas e dicas de ouro para você mandar bem nos concursos públicos. Entender noções de conjuntos é essencial para ganhar agilidade e conquistar pontos importantes nas provas de concursos públicos.
Então, bora lá dominar esse tema de uma vez por todas?
Entendendo o Conceito de Conjunto em Concursos Públicos
Em termos simples, conjunto é um agrupamento de elementos que compartilham uma característica em comum.
Esses elementos podem ser números, letras, objetos, pessoas, animais ou qualquer outra categoria que você imaginar!
Veja alguns exemplos clássicos que costumam aparecer em questões de concursos públicos:
- O conjunto de vogais da língua portuguesa é representado por {a, e, i, o, u}.
- O conjunto de números naturais menores que 5 é {0, 1, 2, 3, 4}.
Sempre que formamos um conjunto, usamos chaves { } para indicar os elementos que o compõem.
🔵 Importante para concursos públicos:
Para que um agrupamento seja considerado um conjunto, seus elementos precisam ser bem definidos.
Ou seja, não pode haver dúvidas sobre a presença ou ausência de um item no grupo. Um conjunto deve ter clareza e objetividade.
Exemplo de agrupamento mal definido (não é um conjunto):
- “O conjunto das pessoas inteligentes” — o conceito de inteligência é subjetivo e, por isso, esse agrupamento não forma um conjunto matemático válido.
Já em provas de concursos públicos, a matemática exige conjuntos objetivos e exatos, como:
- “O conjunto dos números pares entre 1 e 10” → {2, 4, 6, 8, 10}
Dominar os conceitos de noções de conjuntos é fundamental para ter sucesso nas provas de concursos públicos, pois esse tema é base para resolver questões de análise de dados, probabilidade e raciocínio lógico.
Como Representamos Conjuntos?
Na matemática, usamos algumas regrinhas para representar conjuntos:
- Conjuntos: letra maiúscula (A, B, C…).
- Elementos: letra minúscula (a, b, c…).
Exemplo:
Seja o conjunto A = {1, 2, 3}.
Então:
- 1 ∈ A (lê-se “1 pertence a A”).
- 4 ∉ A (lê-se “4 não pertence a A”).
Esses símbolos aparecem muito em provas de concursos públicos, então é bom decorar:
| Símbolo | Significado |
| ∈ | Pertence |
| ∉ | Não pertence |
Tipos de Conjuntos Que Você Precisa Conhecer
Existem alguns tipos básicos de conjuntos que você deve dominar:
🔹 Conjunto vazio ( ∅ ou { } ): conjunto sem nenhum elemento.
🔹 Conjunto unitário: conjunto com apenas um elemento ( ex: {10} ).
🔹 Conjunto finito: conjunto com número limitado de elementos ( ex: {2, 4, 6} ).
🔹 Conjunto infinito: conjunto que nunca termina ( ex: {1, 2, 3, 4, … 1000…} ).
🔹 Conjunto universal (U): o conjunto de todos os elementos possíveis naquele contexto.
Relações Entre Conjuntos: Incluído ou Não?
Algumas relações entre conjuntos caem bastante:
- Inclusão (⊂): o conjunto A está contido em B se todo elemento de A também for de B.
Exemplo: Se A = {1, 2} e B = {1, 2, 3, 4}, então A ⊂ B.
Disjunção: conjuntos disjuntos não têm elementos em comum. Exemplo: o conjunto de frutas {maçã, banana} e o conjunto de animais {gato, cachorro}.
Igualdade (A = B): dois conjuntos são iguais se tiverem exatamente os mesmos elementos.
Operações Entre Conjuntos: Um Assunto Queridinho dos Concursos Públicos
Se você está focado em concursos públicos, anota aí: operações entre conjuntos são figurinha carimbada nas provas!
As principais operações que você deve dominar são:
União de Conjuntos (∪)
União é juntar todos os elementos de dois conjuntos, sem repetir.
Exemplo:
Seja A = {1, 2, 3} e B = {3, 4, 5}.
Então:
A ∪ B = {1, 2, 3, 4, 5}.
(Perceba que o número 3 apareceu nos dois conjuntos, mas só entra uma vez na união!)
Interseção de Conjuntos (∩)
A interseção reúne apenas os elementos que os conjuntos têm em comum.
Exemplo:
A = {a, b, c}
B = {b, c, d}
A ∩ B = {b, c}
Diferença de Conjuntos (\)
A diferença entre dois conjuntos pega os elementos que estão no primeiro conjunto, mas não estão no segundo.
Exemplo:
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
A \ B = {1, 2}
(B \ A = {5, 6})
Repare que:
- A \ B é diferente de B \ A.
Cuidado nas provas de concursos públicos: esse detalhe pega muitos candidatos!
Complemento de um Conjunto
O complemento de um conjunto A em relação ao conjunto universal U é tudo que está em U mas não está em A.
Exemplo:
U = {a, b, c, d, e}
A = {a, c, e}
Então o complemento de A, que escrevemos como A’, é:
A’ = {b, d}
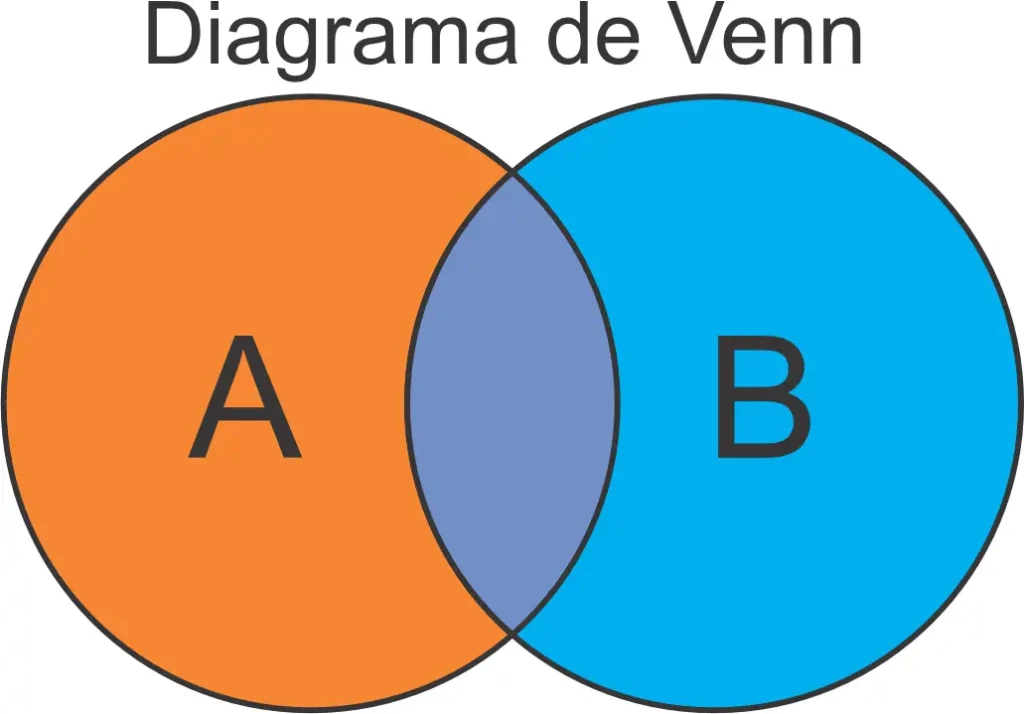
Diagrama de Venn: A Melhor Ferramenta Visual Para Entender Conjuntos em Concursos Públicos
O Diagrama de Venn é uma representação gráfica muito utilizada para ilustrar a relação entre diferentes conjuntos. Ele é composto por círculos ou bolinhas que se cruzam, onde cada círculo representa um conjunto. Esses cruzamentos entre os círculos ajudam a visualizar de forma clara os elementos em comum ou exclusivos de cada conjunto. Ele serve para visualizar:
- Quantos elementos estão em cada grupo.
- Quantos elementos estão na interseção.
- Quantos estão em apenas um grupo.
Exemplo visual simples:
🟠 A = Alunos que gostam de matemática.
🔵 B = Alunos que gostam de português.
O cruzamento dos círculos mostra quem gosta de ambos.
Exemplos Completos Usando Diagramas com foco em Concursos Públicos
🔹 Exemplo:
- 30 alunos jogam futebol (F).
- 20 alunos jogam vôlei (V).
- 10 jogam os dois.
Pergunta: Quantos jogam só futebol?
Resolução com diagrama:
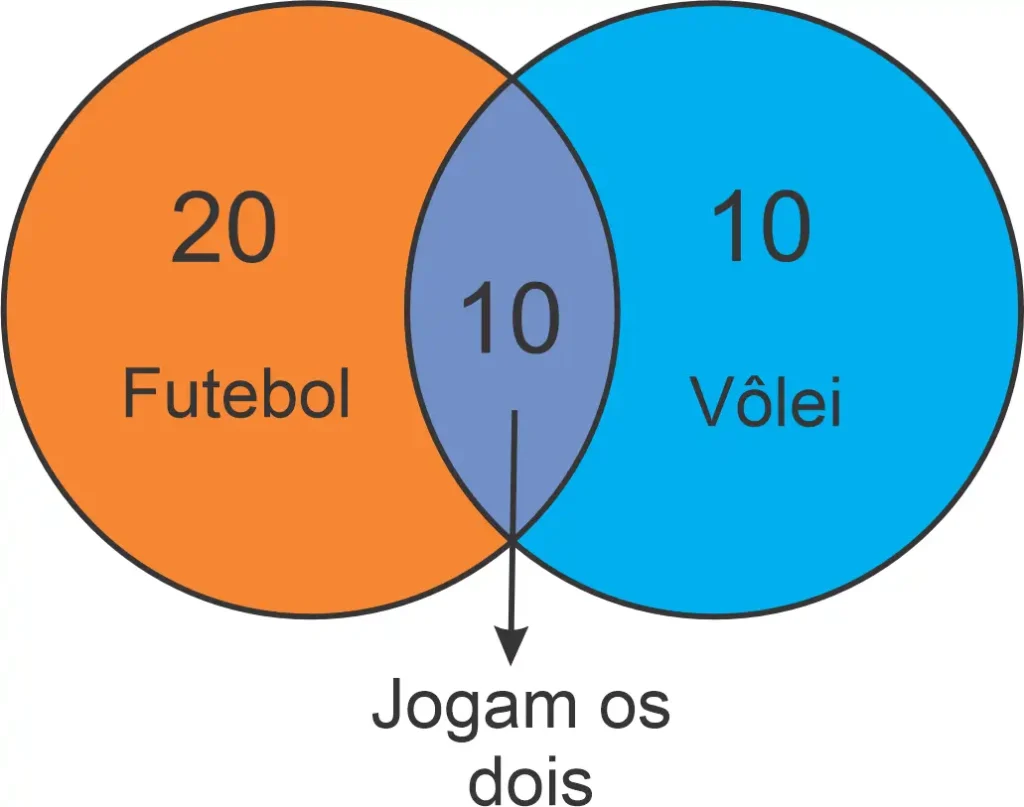
Ao montar o Diagrama de Venn, percebe-se que 10 alunos praticam ambos os esportes. Logo, para calcular o número de alunos que praticam apenas futebol, devemos subtrair os 10 alunos que praticam ambos os esportes do total de 30, o que resulta em 20 alunos que praticam somente futebol. Da mesma forma, para o vôlei, ao subtrair os 10 alunos que praticam ambos os esportes do total de 20, obtemos 10 alunos que praticam somente vôlei. Portanto, a resposta para a questão é que 20 alunos praticam apenas futebol.
Abaixo, segue o Diagrama de Venn ilustrando essa distribuição:
Questão de Concursos Públicos Resolvidas Sobre Noções de Conjuntos
Agora é hora de praticar!
Trouxe aqui uma questão de concurso resolvida e explicada passo a passo.
Questão – Concurso: IBGE (adaptado)
Em uma pesquisa feita com 100 pessoas:
- 60 disseram gostar de café.
- 40 disseram gostar de chá.
- 20 disseram gostar de ambos.
Quantas pessoas não gostam nem de café nem de chá?
Resolução:
Ao desenhar o Diagrama de Venn, percebe-se que 20 pessoas gostam de ambos os itens (café e chá).
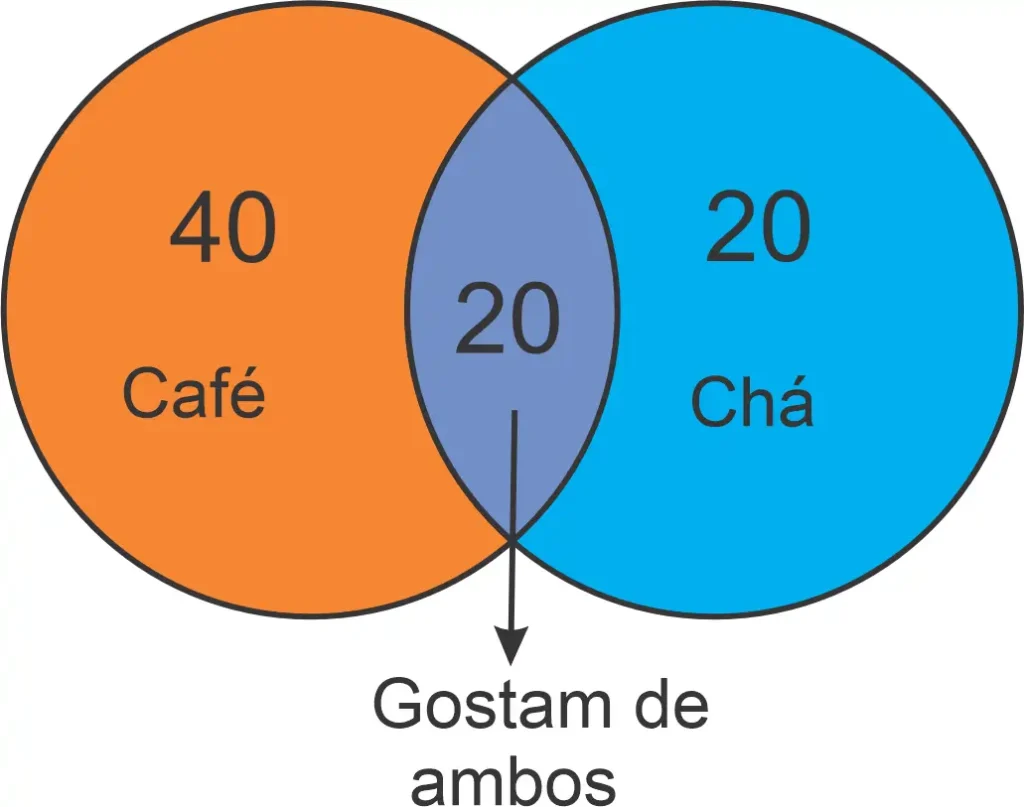
Logo, ao subtrair essas 20 pessoas do total de 60 pessoas que gostam de café, obtemos 40 pessoas que gostam apenas de café. Da mesma forma, ao subtrair as 20 pessoas que gostam de ambos do total de 40 pessoas que gostam de chá, obtemos 20 pessoas que gostam apenas de chá.
Agora, para calcular o número total de pessoas que gostam de pelo menos um dos dois, somamos: 40 (gostam apenas de café) + 20 (gostam apenas de chá) + 20 (gostam de ambos) = 80 pessoas.
Portanto, as pessoas que não gostam nem de café nem de chá são:
100 (total de pessoas) – 80 = 20 pessoas.
✅ Resposta: 20 pessoas.
Dica de Ouro: Como Estudar Conjuntos Para Concursos Públicos?
Se liga:
Muitos candidatos erram essas questões porque NÃO DESENHAM o Diagrama de Venn na hora da prova.
🔵 Então a dica é:
Sempre que aparecer “alunos que gostam de A e B”, “pessoas que fazem X e Y”, desenhe o diagrama!
Fica muito mais fácil ver as relações.
Recapitulando o que você aprendeu hoje para mandar bem nos Concursos Públicos
✔️ O que são conjuntos e como representá-los.
✔️ Operações fundamentais: união, interseção, diferença e complemento.
✔️ Como usar Diagramas de Venn para resolver questões.
✔️ Exemplos reais de provas de concursos públicos resolvidos.
✔️ Dicas práticas de estudo focadas para concursos.
Última Motivação: Você é Capaz!
Se tem algo que aprendi nessa jornada de estudo para concursos públicos, é que a persistência sempre vence.
Matemática, assim como qualquer outra disciplina, é questão de prática constante.
Então:
- Faça muitos exercícios.
- Não tenha medo de errar.
- Use diagramas sempre que puder.
E nunca se esqueça:
Conjuntos é um assunto considerado “fácil” nas provas. Ou seja, é um tema onde você pode e deve garantir pontos.
Bons estudos! 🚀
“Quer praticar com questões sobre Noções de Conjuntos? Acesse aqui e resolva exercícios para reforçar seus estudos!”
Dica de Livro para otimizar o seu estudo
Se você procura um material claro e direto para aprender matemática voltada para concursos, esse livro é uma ótima escolha. Com explicações simples, exercícios resolvidos e acesso a videoaulas, ele é ideal para quem quer dominar o conteúdo com praticidade. Confira na Amazon.





















