Entenda de forma fácil o que é permutação simples e permutação com repetição, dois temas muito cobrados em provas de matemática e concursos públicos. Aprenda a identificar quando usar cada tipo, como aplicar as fórmulas corretas e veja exemplos práticos que ajudam a fixar o conteúdo. Descubra também como calcular anagramas com e sem letras repetidas, como no caso da palavra “CONCURSO”. Estude com explicações claras, passo a passo, e domine a combinatória sem complicação!
Permutação Simples
Você já parou pra pensar em quantas maneiras diferentes dá pra organizar um grupo de coisas? Pois é, isso tem um nome: permutação simples. Aqui no site, a gente vai conversar bastante sobre esse conceito que faz parte da combinatória e que aparece direto em provas de matemática, vestibulares e também em concurso público.
De forma bem simples, a permutação simples é quando você quer saber de quantas formas pode ordenar elementos de um conjunto, sem repetir e levando em conta a ordem. Parece complicado? Fica tranquilo, porque por aqui eu explico tudo de um jeito fácil, com exemplos, passo a passo e muitos exercícios resolvidos pra você entender de vez como funciona a permutação simples — e mandar bem na sua prova, seja ela do colégio, do vestibular ou de um concurso público
Exemplo de permutação simples para concursos
Imagine que você tem 3 letras diferentes: A, B e C.
A pergunta é: de quantas formas diferentes podemos organizar essas letras, sem repetir nenhuma, e levando em conta a ordem?
Vamos listar todas as possibilidades:
- ABC
- ACB
- BAC
- BCA
- CAB
- CBA
Nesse caso, temos 6 formas diferentes de organizar as letras.
Essas 6 formas são as permutações simples das letras A, B e C.
E como a gente calcula isso sem precisar listar tudo? Usando o fatorial do número de elementos:
Permutação simples de 3 elementos = 3! = 3 × 2× 1 = 6
Esse tipo de raciocínio é muito comum em questões de concurso público e provas de matemática
Permutação com elementos repetidos
Quando falamos de permutação simples, a ideia é organizar elementos diferentes em todas as possíveis ordens. Mas e quando alguns desses elementos se repetem? É aí que entra a permutação com elementos repetidos.
Imagina o seguinte: se você tem uma palavra como “CONCURSO”, percebe que algumas letras aparecem mais de uma vez, como o C e o O. Se a gente usasse a mesma fórmula da permutação simples, acabaria contando várias vezes a mesma combinação, só porque trocou a ordem de letras iguais. E isso não faz sentido, né?
Por isso, a permutação com elementos repetidos serve exatamente pra corrigir isso. A gente calcula todas as possibilidades como se as letras fossem diferentes e depois divide pelas repetições. Dessa forma, só conta as ordens que realmente formam anagramas diferentes.
Esse tipo de permutação aparece muito em exercícios de anagramas, principalmente em provas de matemática, vestibulares e concurso público. Entender esse conceito ajuda bastante a evitar erros bobos e a economizar tempo na hora da prova.
A ideia por trás da fórmula:
Quando você tem elementos repetidos, não faz sentido contar todas as trocas de lugar dessas partes iguais como se fossem diferentes. Por isso, a gente divide o total de permutações pelas repetições.
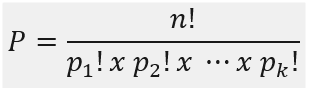
Onde:
- n! é o fatorial do número total de elementos (letras, números, objetos…)
- p₁!, p₂!, …, pₖ! são os fatoriais das quantidades de elementos repetidos
Exemplo com a palavra “CONCURSO”
Vamos lá. A palavra CONCURSO tem 8 letras:
C – O – N – C – U – R – S – O
Mas olha só: nem todas são diferentes. Repare:
- A letra C aparece 2 vezes
- A letra O aparece 2 vezes
- As demais (N, U, R, S) aparecem 1 vez cada
Se todas as letras fossem diferentes, a gente faria:
8! = 40.320
Mas como tem letras repetidas, a gente precisa dividir o total de permutações pelas repetições. Isso evita contar como diferentes palavras que só mudaram a ordem de letras iguais.
Para o exemplo da palavra CONCURSO fica:
- 8! → total de letras
- 2! → para as duas letras C
- 2! → para as duas letras O
A fórmula fica assim:
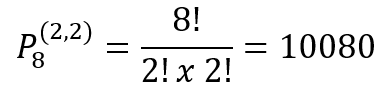
logo, a palavra CONCURSO tem 10.080 anagramas diferentes.
✅ Conclusão
Agora que você entendeu como funciona a permutação simples e a permutação com repetição, já está um passo à frente na hora de resolver questões de combinatória em provas de matemática e concursos públicos. Lembre-se: identificar corretamente o tipo de permutação e aplicar a fórmula certa faz toda a diferença no resultado. Continue praticando com exemplos variados e, sempre que surgir dúvida, volte aqui — o conteúdo foi feito pra te ajudar a aprender de verdade e conquistar a sua vaga!
“Quer praticar com questões sobre o Princípio Fundamental da Contagem? Acesse aqui e resolva exercícios para reforçar seus estudos!”
Dica de Livro para otimizar o seu estudo
Se você procura um material claro e direto para aprender matemática voltada para concursos, esse livro é uma ótima escolha. Com explicações simples, exercícios resolvidos e acesso a videoaulas, ele é ideal para quem quer dominar o conteúdo com praticidade. Confira na Amazon.




















