Se você está se preparando para um concurso público, precisa dominar os principais temas de matemática básica — e um dos assuntos que mais caem nas provas é a Progressão Aritmética, também conhecida pela sigla P.A..

Neste guia completo, você vai aprender o que é uma Progressão Aritmética, como identificar seus elementos, aplicar as fórmulas mais cobradas e resolver exercícios comentados de concursos anteriores. Tudo isso com uma linguagem simples, direta e cheia de dicas práticas para não errar nas questões!

🎯 O que é uma Progressão Aritmética (P.A.)? Entenda de forma simples e definitiva!

A Progressão Aritmética (P.A.) é um tipo de sequência numérica muito cobrada em concursos públicos, especialmente na parte de matemática básica. Nela, cada termo (ou número) é obtido somando sempre o mesmo valor ao termo anterior.

Esse valor constante é chamado de razão da P.A. e costuma ser representado pela letra r.

📌 Definição formal:

Uma P.A. é uma sequência do tipo:
a₁, a₂, a₃, a₄, …
em que a diferença entre dois termos consecutivos é sempre a mesma. Essa diferença é calculada assim:

ou seja, razão = termo atual – termo anterior

✅ Exemplo prático:

Sequência: 2, 5, 8, 11, 14, …

Vamos observar:

• 5 – 2 = 3
• 8 – 5 = 3
• 11 – 8 = 3
• 14 – 11 = 3

🔍 A razão r é 3, pois estamos sempre acrescentando 3 ao termo anterior.

Portanto, essa sequência é uma Progressão Aritmética de razão 3.

🧠 Dica importante para concursos:

Nem toda P.A. começa com o número 1 ou com número positivo. A razão também pode ser negativa ou até igual a zero. Veja:

• P.A. decrescente: 20, 15, 10, 5, 0… → r = –5
• P.A. constante: 4, 4, 4, 4… → r = 0

✅ Em todos os casos, o que define a P.A. é que a diferença entre os termos seja constante, independentemente de ela ser positiva, negativa ou nula.

📌 Elementos da Progressão Aritmética

Para resolver questões de P.A., é fundamental entender os elementos que compõem essa sequência. Veja os principais:

• a₁: é o primeiro termo da P.A.
• r: é a razão da progressão (a diferença entre os termos).
• n: é o número de termos.
• aₙ: é o n-ésimo termo (ou termo geral).

🧮 Fórmula do Termo Geral da P.A.

Essa fórmula permite descobrir qualquer termo da sequência, sem precisar escrever todos os anteriores.

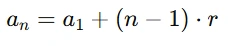
🔍 Como usar essa fórmula?
Basta saber o primeiro termo (a₁), a razão (r) e a posição (n) do termo que você quer encontrar.

✅ Exemplo comentado:

Dada a P.A.: 7, 10, 13, 16, …
Qual é o 12º termo (a₁₂)?

Solução:

• a₁ = 7
• r = 3
• n = 12

Aplicando na fórmula:

✅ Resposta: O 12º termo é 40.

➕ Fórmula da Soma dos Termos da P.A.

Se precisar somar os termos de uma P.A., use:

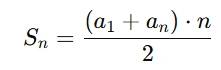
Ou, se você não souber o termo aₙ:

✅ Exemplo de soma:

Qual é a soma dos 20 primeiros termos da P.A.: 3, 6, 9, 12, …?

Solução:

• a₁ = 3
• r = 3
• n = 20

Primeiro, achamos o 20º termo:

Agora aplicamos na fórmula da soma:

✅ Resposta: A soma dos 20 primeiros termos é 630.

🚨 Dicas que caem em concursos:

• Se a razão for positiva, a P.A. é crescente.
• Se a razão for negativa, a P.A. é decrescente.
• Se a razão for zero, todos os termos são iguais (P.A. constante).
• A fórmula do termo geral ajuda a calcular qualquer termo, mesmo que esteja longe do início.

❗ Atenção às pegadinhas em concursos públicos!

Ao resolver questões de Progressão Aritmética (P.A.) em provas de concurso público, é comum encontrar pegadinhas criadas para confundir o candidato. Veja os erros mais frequentes:

⚠️ Principais armadilhas:

• Confundir posição com valor:
  A posição (n) indica qual termo da sequência está sendo tratado (1º, 5º, 10º…), enquanto aₙ é o valor numérico daquele termo.
  → Exemplo: “Qual é o 5º termo?” (n = 5), mas o valor de a₅ será calculado usando a fórmula.
• Trocar fórmulas com outros conteúdos, como Progressão Geométrica (P.G.).
  As fórmulas de P.A. são lineares, enquanto na P.G. envolvem potenciação.
  → Se aparecer algo como “aₙ = a₁ · qⁿ⁻¹”, cuidado! Isso é fórmula de P.G., não de P.A.
• Solicitar termos centrais ou intermediários:
  Em P.A. com número ímpar de termos, o termo do meio pode ser calculado de forma direta.
  → Dica: em uma P.A. com 9 termos, o termo central é o 5º (porque é o “meio” de 1 a 9).
  Em provas, isso pode ser perguntado de forma indireta, como: “qual é o termo que ocupa a posição central?”

✅ Dica essencial para evitar erros:

Antes de qualquer conta, identifique claramente os dados fornecidos pela questão:

• Qual é o primeiro termo (a₁)?
• Qual é a razão (r)?
• Qual é a posição (n)?
• Estão pedindo o termo aₙ ou a soma Sₙ?

💡 Organizar as informações no início da resolução ajuda a evitar confusões e acelera o raciocínio.

🎯 Conclusão

Dominar Progressão Aritmética é essencial para quem estuda para concurso público. Neste conteúdo, você aprendeu:

• O que é uma P.A. e seus elementos principais;
• Como aplicar a fórmula do termo geral;
• Como calcular a soma dos termos da sequência;
• E viu um exemplo de prova comentado, com explicação passo a passo.

“Quer praticar resolvendo mais questões sobre Progressão Aritmética? Acesse aqui e resolva exercícios para reforçar seus estudos!”

Gostaria de ver mais exercícios comentados sobre Progressão Aritmética, acesse a nossa sessão de exercícios comentados e turbine os seus estudos.