🏦 Introdução ao Sistema Price
Provavelmente, se você já lidou com financiamentos, compras parceladas ou simulações de empréstimo no banco, já se deparou com o Sistema de Amortização Price, também conhecido como Tabela Price ou Sistema Francês (SAF).”
E olha — esse assunto que cai muito em concurso público, principalmente em provas bancárias (como Banco do Brasil, Caixa e BNDES) e também em concursos da área administrativa ou financeira. Então, se você quer garantir uns pontinhos fáceis, precisa entender como esse sistema funciona.
Mas calma! 😅 Apesar do nome parecer complicado, a ideia do Sistema Price é bem simples:
👉 Ele é aquele sistema em que as parcelas são sempre iguais, do começo ao fim do financiamento.
Ou seja, se você pegou um empréstimo e vai pagar em 12 meses, o valor da prestação mensal não muda.
A diferença está dentro de cada parcela — porque ela é composta por duas partes:
- Juros (o que o banco ganha)
- Amortização (a parte que realmente abate a sua dívida 💰).
No começo, os juros são altos e a amortização é pequena.
Com o tempo, a amortização cresce e os juros diminuem.
Mas o valor total da prestação permanece igual — e é isso que caracteriza o sistema Price.
🔹 Resumindo:
“No Sistema Price, o valor da prestação é fixo, mas a composição dela (juros + amortização) muda a cada mês.”
Quer mandar bem em matemática nos concursos?
👉 Clique aqui e explore mais conteúdos essenciais para turbinar seus estudos!
🧠 Por que esse assunto aparece em concurso público?
Simples! Porque ele envolve matemática financeira, juros compostos e interpretação de fórmulas — três coisas que as bancas adoram cobrar.
As questões normalmente pedem para:
- Calcular o valor da prestação (PMT);
- Descobrir quanto foi pago de juros ou amortização em certo mês;
- Comparar com outros sistemas (como o SAC, em que as parcelas diminuem).
E o segredo pra não errar está em entender a lógica antes da fórmula.
A fórmula vem depois — e, se você entende o raciocínio, nem precisa decorar à força.
💬 Um exemplo rápido pra clarear a mente:
Imagina que o João pegou R$ 1.000 emprestado no banco pra pagar em 4 parcelas mensais, com juros de 10% ao mês.
- No Sistema Price, todas as parcelas terão o mesmo valor, digamos que R$ 315,47 cada (a gente vai aprender a calcular isso direitinho depois).
- Mas na primeira parcela, boa parte disso será juros, e só uma parte pequena será amortização (ou seja, o quanto a dívida de fato diminui).
- Já lá na última parcela, quase tudo será amortização, e os juros serão bem pequenos.
👉 No final das contas, ele paga sempre R$ 315,47, mas o que muda é quanto vai para o banco e quanto reduz a dívida.
🧩 Curiosidade rápida:
A “Tabela Price” leva esse nome por causa de Richard Price, um matemático e filósofo inglês do século XVIII.
Ele foi um dos primeiros a estudar juros compostos e aplicações financeiras.
Mas no Brasil, a Tabela Price ficou famosa mesmo por causa dos financiamentos de carros e imóveis, já que quase todos os bancos usam esse sistema até hoje.
💡 Como funciona o Sistema Price na prática
Agora que você já entendeu o conceito básico do Sistema Price — parcelas fixas, mas composição variável (juros + amortização) —, vamos colocar a mão na massa pra entender como isso acontece na prática.
Pensa assim: o banco te empresta um dinheiro, e você vai devolver esse dinheiro aos poucos, pagando juros sobre o saldo que ainda falta quitar.
Com o passar do tempo, o saldo vai diminuindo, então os juros também caem.
Mas como o valor da parcela (prestação) é sempre igual, o que acontece é que:
- No início, a parte dos juros é grande e a amortização é pequena;
- No fim, acontece o contrário: os juros ficam pequenos e a amortização fica maior.
🎯 Essa é a mágica do Sistema Price.
📊 Estrutura da Parcela
Cada prestação é formada assim:
Prestação (PMT) = Juros + Amortização
E essas duas partes mudam mês a mês.
O total que você paga (PMT) é fixo, mas o quanto vai para os juros e o quanto vai para a dívida varia.
🧩 Entendendo o papel de cada parte:
- Juros: são calculados sobre o saldo devedor do mês anterior.
Juros = Saldo Devedor Anterior x i
- Amortização: é o que sobra da parcela depois de pagar os juros.
Amortização = PMT – Juros
- Novo saldo devedor: é o saldo anterior menos a amortização.
Saldo Novo = Saldo Anterior – Amortização
🧮 Mas de onde vem o valor da prestação (PMT)?
É aqui que entra a famosa fórmula da Tabela Price:
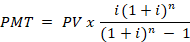
Onde:
- PMT = valor da prestação (a parcela fixa);
- PV = valor presente (o valor financiado ou emprestado);
- i = taxa de juros por período (geralmente ao mês);
- n = número total de parcelas.
💬 Vamos traduzir isso pro “português de concurso”:
- O PV é o valor do empréstimo (quanto você pegou no banco).
- O i é o juros mensal. Se for 10%, vira 0,10 na fórmula.
- O n é quantas vezes você vai pagar (número de meses).
- E o resultado (PMT) é quanto você vai pagar todo mês.
Simples assim.
O segredo é aplicar direitinho a fórmula e não se atrapalhar com os parênteses.
⚙️ Exemplo rápido pra entender a mecânica:
Imagine que a Maria pegou um empréstimo de R$ 1.000,00 pra pagar em 4 meses, com juros de 10% ao mês.
Vamos calcular o valor da prestação (PMT):
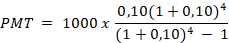
Primeiro, resolvemos o que está dentro dos parênteses:
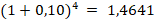
Agora substituímos:
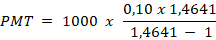
= 315,47
👉 Então a Maria vai pagar 4 parcelas de R$ 315,47.
Percebe? O valor da parcela é fixo, mas internamente cada uma tem juros e amortização diferentes.
📘 Montando uma mini tabela de amortização
Pra ver isso melhor, olha como ficariam as 4 parcelas (valores aproximados):
| Parcela | Saldo Devedor Anterior | Juros (10%) | Amortização | Prestação (PMT) | Saldo Final |
| 1 | 1000,00 | 100,00 | 215,47 | 315,47 | 784,53 |
| 2 | 784,53 | 78,45 | 237,02 | 315,47 | 547,51 |
| 3 | 547,51 | 54,75 | 260,72 | 315,47 | 286,79 |
| 4 | 286,79 | 28,68 | 286,79 | 315,47 | 0,00 |
🔎 Repare:
- A prestação é sempre R$ 315,47.
- Os juros diminuem a cada mês.
- A amortização aumenta progressivamente.
- No fim, a dívida chega a zero.
Esse é o comportamento clássico da Tabela Price.
💭 Comparando com outros sistemas
Pra não confundir na prova, vale lembrar:
| Sistema | Parcelas | Amortização | Juros |
| Price | Iguais | Crescente | Decrescente |
| SAC | Decrescentes | Iguais | Decrescentes |
| SAM | Crescentes | Crescentes | Decrescentes |
Então, se a questão falar “parcelas iguais”, pode apostar que é o Sistema Price!
⚠️ Cuidado com pegadinhas de prova!
Algumas bancas tentam confundir o candidato:
- Dão o valor total pago e pedem pra achar o valor da prestação.
- Pedem o valor de juros pagos até certo mês.
- Ou trocam o período de juros (mensal x anual).
Por isso, nunca se esqueça de uniformizar as taxas — se o financiamento é em meses, a taxa tem que estar ao mês também!
🔢 Passo a passo para calcular as parcelas
Até aqui você já entendeu que no Sistema Price as parcelas são iguais, e que o valor da prestação (PMT) é calculado com uma fórmula específica.
Agora vamos ver como realmente calcular e montar a tabela passo a passo, como se fosse uma questão de concurso público.
🎯 O que você precisa saber antes de começar:
Sempre que aparecer uma questão de Sistema Price, anote mentalmente esse checklist:
- 💰 Valor financiado (PV) – quanto o cliente pegou emprestado.
- 📅 Número de parcelas (n) – quantas vezes vai pagar.
- 📈 Taxa de juros (i) – sempre uniformize! (ao mês, se o prazo for mensal).
- 🔢 Fórmula da prestação (PMT) –
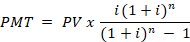
💡 Passo 1: Calcular o valor da prestação
Esse é o ponto de partida.
Vamos usar um exemplo completo:
Exemplo:
Um cliente financiou R$ 10.000,00 para pagar em 6 parcelas mensais com juros de 2% ao mês pelo Sistema Price.
Calcule o valor da prestação mensal.
Passo 1 — Aplicar a fórmula:
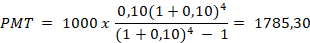
✅ Valor da prestação: R$ 1.785,30 (fixa todo mês).
💡 Passo 2: Calcular os juros do 1º mês
Os juros do primeiro mês são calculados sobre o valor total do empréstimo:
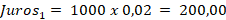
💡 Passo 3: Calcular a amortização do 1º mês
Lembra da relação:
Amortização = PMT – Juros
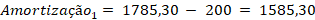
💡 Passo 4: Atualizar o saldo devedor
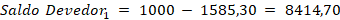
💡 Passo 5: Repetir o processo até quitar o saldo
Vamos montar a tabela resumida até o final:
| Parcela | Saldo Devedor Anterior | Juros (2%) | Amortização | Prestação (PMT) | Saldo Final |
| 1 | 10.000,00 | 200,00 | 1.585,30 | 1.785,30 | 8.414,70 |
| 2 | 8.414,70 | 168,29 | 1.617,01 | 1.785,30 | 6.797,69 |
| 3 | 6.797,69 | 135,95 | 1.649,35 | 1.785,30 | 5.148,34 |
| 4 | 5.148,34 | 102,97 | 1.682,33 | 1.785,30 | 3.466,01 |
| 5 | 3.466,01 | 69,32 | 1.715,98 | 1.785,30 | 1.750,03 |
| 6 | 1.750,03 | 35,00 | 1.750,30 | 1.785,30 | 0,00 |
🧠 O que você deve observar nessa tabela:
- A prestação (R$ 1.785,30) é constante.
- Os juros vão caindo mês a mês.
- A amortização vai subindo.
- E no final o saldo devedor chega a zero, como esperado.
📌 Passo 6: Revisando a lógica
Vamos entender de novo o que acontece:
- No início, a dívida é alta → os juros também são altos.
- Conforme você paga, o saldo devedor cai → os juros diminuem.
- A diferença (a parte da parcela que “sobra”) vira amortização.
Ou seja, você paga o mesmo valor todo mês, mas vai devendo cada vez menos.
É por isso que o sistema é tão usado em financiamentos de longo prazo, como casas e carros.
💬 Resumo do passo a passo:
- Use a fórmula do PMT pra achar o valor da parcela.
- Calcule os juros sobre o saldo anterior.
- Subtraia os juros da parcela pra achar a amortização.
- Subtraia a amortização do saldo devedor pra achar o novo saldo.
- Repita até zerar a dívida.
🧾 Dica prática de memorização
Um jeito fácil de lembrar da fórmula da PMT é o “copo de refrigerante”:
- O valor presente (PV) é o “líquido”.
- A taxa (i) é o “gás”.
- O número de parcelas (n) é o “tempo que o gás dura”.
Quanto mais tempo, mais o gás se espalha — e o valor da parcela fica mais equilibrado ao longo do tempo. 😄
Exercício de Concurso Público Resolvido
Vamos resolver um exercício para consolidar o que você aprendeu”
Exercício — Um cliente tomou R$ 5.000,00 emprestados pelo Sistema Price para pagar em 8 parcelas mensais. A taxa de juros é de 1,5% ao mês.
Calcule:
a) o valor da prestação mensal (PMT);
b) quanto foi pago de juros na 3ª parcela;
c) qual o saldo devedor após o pagamento da 5ª parcela.
✅ Resolução — raciocínio primeiro
Para a resolução deste exercício, foi considerado duas casas após a virgulas para simplificar os cálculos.
No Sistema Price:
- a parcela (PMT) é fixa e dada por:
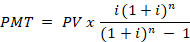
onde PV = 5000, i = 0,015 e n = 8.
Vamos calcular o PMT, montar os primeiros meses da tabela (juros, amortização, saldo) e então responder (b) e (c).
1) Calcular a prestação (PMT)
Passos detalhados:
- Calcule
=
- Calcule o numerador
- Substitua na fórmula
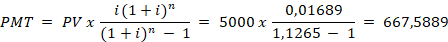
Apresentando em reais e centavos (arredondando para 2 casas):
PMT = R$ 667,60
2) Montar os primeiros meses da tabela (usar PMT com precisão interna)
A lógica mensal:
- Juros do mês = saldo anterior × i
- Amortização = PMT − juros
- Novo saldo = saldo anterior − amortização
Mês 0 (inicial): saldo = R$ 5.000,00
Mês 1
- Juros1 = 5.000 × 0,015 = 75,00
- Amortização1 = PMT − juros = 667,60 − 75,00 ≈ 592,60
- Saldo após 1ª = 5.000 − 592,60 ≈ 4.407,40
Mês 2
- Juros2 = 4.407,40× 0,015 = 66,11
- Amortização2 = PMT − juros = 667,60 – 66,11 ≈ 601,49
- Saldo após 2ª = 4.407.40 – 601,49 ≈ 3.805,91
Mês 3
- Juros3 = 3.805,91 × 0,015 = 57,09
- Amortização3 = PMT − juros = 667,60 – 57,09 ≈ 610,51
- Saldo após 3ª = 3.805,91 – 610,51 ≈ 3.195,40
Mês 4
- Juros4 = 3,191,40 × 0,015 = 47,93
- Amortização4 = PMT − juros = 667,60 – 47,93 ≈ 619,67
- Saldo após 4ª = 3,191,40 – 619,67 ≈ 2.571,73
Mês 5
- Juros5 = 2.571,73 × 0,015 = 38,58
- Amortização5 = PMT − juros = 667,60 – 38,58 ≈ 629,02
- Saldo após 5ª = 2.571,73 – 629,02 ≈ 1.942,71
(Continuando até o mês 8 a dívida zera — checagem final: depois da 8ª parcela o saldo é praticamente zero.)
3) Respostas (comentário rápido)
a) Prestação mensal (PMT):
R$ 667,60
b) Juros pagos na 3ª parcela: usamos Juros3_33 calculado acima:
R$ 57,09
c) Saldo devedor após a 5ª parcela: conforme o cálculo do mês 5:
R$ 1.942,71
💡 Dicas para a prova
- Ao calcular juros mensais, não arredonde até o final; arredonde apenas ao mostrar o resultado (centavos). Isso evita erros por acumulação.
- Se a questão pede “valor aproximado”, mantenha 2 casas decimais, mas saiba que a banca aceita pequenas variações (±1 centavo) dependendo do método de arredondamento.
- Identificou “parcelas iguais”? Pense imediatamente em Price — a fórmula do PMT resolve a maior parte das questões.
📈 Dicas para acertar questões de Sistema Price em Concurso Público
Beleza, você já entendeu toda a teoria: sabe o que é a Tabela Price, conhece a fórmula, viu como calcular juros, amortização e saldo.
Mas na hora da prova… o tempo é curto ⏱️ e o examinador adora testar se você realmente entendeu o conceito.
Então, se liga nessas dicas práticas e diretas que vão te ajudar a acertar mesmo sob pressão.
💡 Identifique o sistema logo de cara
Antes de fazer qualquer conta, leia o enunciado com calma.
Se ele falar algo do tipo:
- “as prestações são fixas”, ou
- “as parcelas mensais são de mesmo valor”,
➡️ já marca mentalmente: Sistema Price.
Se, em vez disso, disser “as amortizações são iguais”, aí é SAC.
Simples assim.
Muita gente erra só por não reconhecer o sistema usado.
🧮 Faça o cálculo da PMT primeiro
Mesmo que a questão não peça explicitamente, sempre comece calculando o valor da prestação (PMT).
Por quê?
Porque a partir dela você consegue encontrar juros, amortização e saldo devedor de qualquer mês.
Tudo gira em torno da PMT.
👉 Sem PMT = sem progresso.
💭 Entenda o comportamento das parcelas
Em vez de tentar decorar, pense assim:
| Mês | Juros | Amortização | Prestação |
| Início | Alto | Baixo | Igual |
| Meio | Médio | Médio | Igual |
| Fim | Baixo | Alto | Igual |
Ou seja:
- Juros caem ao longo do tempo;
- Amortização sobe;
- Prestação permanece igual.
📘 Resumo mental:
“No Price, os juros vão emagrecendo e a amortização vai engordando — mas a parcela continua de dieta (fixa).” 😄
⚠️ Evite arredondar cedo demais
Nas provas de matemática financeira, um erro comum é arredondar muito cedo.
Isso pode gerar diferenças pequenas, mas suficientes pra te tirar do gabarito.
💬 Regra de ouro:
Só arredonde no final, na última linha da tabela.
Se a questão permitir, use 4 casas decimais nos cálculos intermediários.
🧠 Quando a questão for conceitual (sem conta)
Nem sempre a banca quer conta.
Às vezes, ela quer interpretação.
Veja um exemplo clássico:
“Em um financiamento pelo sistema Price, o valor das amortizações:
(A) é constante;
(B) cresce ao longo do tempo;
(C) decresce ao longo do tempo;
(D) é igual ao valor da prestação.”
👉 Resposta: (B) Cresce ao longo do tempo.
💬 Dica: Se o enunciado mencionar “prestações iguais” e “amortização variável”, a resposta certa quase sempre envolve crescimento da amortização.
🔍 Compare com outros sistemas
As bancas adoram misturar SAC e Price na mesma prova.
Então, mantenha isso decorado:
| Sistema | Parcelas | Amortização | Juros |
| Price | Iguais | Crescente | Decrescente |
| SAC | Decrescentes | Iguais | Decrescentes |
| SAM | Crescentes | Crescentes | Decrescentes |
📘 Macete rápido:
“No Price, tudo é igual. No SAC, quem é igual é a amortização.”
💬 Use a tabela mental
Você não precisa decorar tabela nenhuma, mas saiba como os valores se comportam.
Por exemplo:
- Primeira parcela → juros altos → amortização pequena.
- Última parcela → juros baixos → amortização alta.
Se o enunciado disser que no 5º mês os juros foram maiores que no 6º, é verdade.
Mas se disser que os juros crescem com o tempo, é falso.
Essas afirmações lógicas são cobradas em provas teóricas de matemática financeira.
📘 Dica de ouro para concursos bancários (BB, Caixa, BNB…)
Essas bancas adoram cobrar o Sistema Price como parte da Matemática Financeira.
Elas pedem, por exemplo:
- O valor pago de juros até o mês 4;
- O valor amortizado até o mês 3;
- O saldo devedor após certo número de parcelas;
- Ou a taxa de juros, dada a prestação e o número de parcelas.
👉 Se você dominar a fórmula e o raciocínio da tabela, acerta todas.
👉 Quer praticar com mais questões sobre Tabela Price? Acesse o nosso Banco de Questões resolva quantos exercícios quiser para reforçar seus estudos!”



















