Ei, você aí que trava quando vê PG na prova! Relaxa, eu te ajudo. Aqui tem uns exercícios resolvidos com aquele passo a passo que seu professor nunca tem tempo de explicar direito. Vamos desenrolar juntos como achar termos, calcular razão e somar tudo nessa bagunça geométrica. Prometo que no final você vai olhar pra essas questões e pensar “ué, mas era só isso?” 😉
1 – [FCC – 2017 – TRT 11ª Região] – Uma PG tem primeiro termo igual a 5 e razão igual a 2. O sexto termo dessa PG é:
a) 160
b) 80
c) 320
d) 640
e) 240
RESOLUÇÃO:
Dados: a1 = 5
q = 2
n = 6
Termo geral da PG:
aₙ = a₁ · q(n – 1)
a6 = 5 · 2(6 – 1)
a6 = 160
✅ Resposta: a) 160
2 – [CESPE – 2018 – SEDUC-AL] – Em uma PG de termos positivos, o 3º termo é 18 e o 5º termo é 162. Nesse caso, a soma dos 6 primeiros termos dessa PG é igual a:
a) 726
b) 728
c) 729
d) 730
RESOLUÇÃO:
Dados: a3 = 18, a5 = 162
Usando o termo geral aₙ = a₁ · q(n – 1) temos?:
a3 = a₁ · q2 (I)
a5 = a₁ · q4 (II)
- Dividindo (II) por (I):
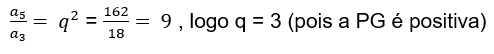
- Substituindo q em (I):
a₁ · 32 = 18 logo, ⟹ a₁ = 2
- Soma dos 6 primeiros termos
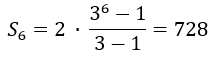
✅ Resposta: b) 728
3 – [VUNESP – 2016 – Prefeitura de SP] – Três números estão em PG crescente. Se a soma deles é 31 e o produto é 125, então o maior desses números é:
a) 15
b) 20
c) 25
d) 30
RESOLUÇÃO:
Passo 1: Representação da PG
Uma PG com 3 termos pode ser escrita na forma:
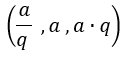
Onde:
a = termo central,
q = razão da PG (q > 1, pois a PG é crescente).
Passo 2: Usar o Produto (Dado = 125)
O produto dos três termos é:
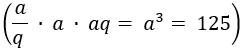
Simplificando temos:
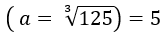
Agora sabemos que o termo central é 5.
Passo 3: Usar a Soma (Dado = 31)
Substitua a = 5 na soma dos termos:
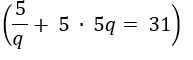
Primeiro iremos subtrair 5 de ambos os lados e em seguida multiplicaremos tudo por q e obteremos a seguinte equação quadrática:
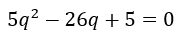
Passo 4: Resolver a Equação Quadrática
Use a fórmula de Bhaskara:
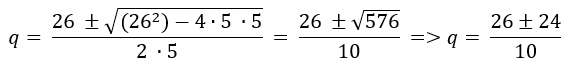
Duas solução são possíveis:
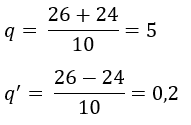
Descartamos a solução q = 0,2 pois a PG é crescente (q > 1)
Logo, q = 5
Passo 5: Encontrar o Maior Termo
Agora, substitua a = 5 e q = 5 na PG:
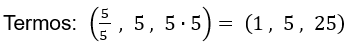
O maior termo é 25.
✅ Resposta: c) 25















