Preparando-se para o concurso público da Caixa Econômica Federal? Você está no lugar certo! Nesta segunda parte da resolução da prova para engenheiro eletricista do concurso da Caixa de 2015, vamos resolver mais 4 exercícios passo a passo, com foco em engenharia elétrica.

Este material foi desenvolvido especificamente para candidatos que buscam aprovação em concursos públicos na área de engenharia elétrica, oferecendo uma preparação direcionada para o concurso da Caixa Econômica e demais seleções para engenheiro eletricista.

O que você encontrará neste guia:

• Resolução detalhada de 4 questões específicas do concurso da Caixa para engenheiro eletricista
• Explicações claras sobre conceitos fundamentais de engenharia elétrica
• Técnicas e estratégias aplicáveis a diversos concursos públicos da área
• Complemento ideal à primeira parte desta série de resoluções

Por que este material é essencial para sua preparação?

A prática com provas anteriores de engenheiro eletricista é fundamental para sua aprovação. Esta análise específica do concurso da Caixa oferece não apenas respostas, mas a metodologia de resolução que você pode aplicar em diversos concursos públicos da área de engenharia elétrica.

Dica importante: Utilize este material não apenas para o concurso da Caixa, mas como base para todos os demais concursos de engenheiro eletricista que estão por vir. Volte sempre que precisar rever algum conceito ou técnica específica.

Não viu a primeira parte? Acesse aqui para ver a resolução detalhada dos primeiros exercícios do concurso da Caixa para engenheiro eletricista e complete sua preparação!

QUESTÃO 20

Considere as perdas de um motor de indução trifásico desde a potência de entreferro até a potência mecânica resultante no eixo do motor.

Essas são compostas pela perda ôhmica do rotor e pelas perdas por atrito e ventilação, podendo desconsiderar as demais perdas.

O motor possui 6 polos e trabalha com frequência de 60Hz. Suponha, ainda, que o motor esteja acoplado a uma carga e que, nessa situação, o escorregamento seja de 2,5%, a potência de entreferro seja de 5.000 W, e as perdas por atrito e ventilação totalizem 312 W.

Nessa situação, qual o torque, em Nm, produzido no eixo do motor?

RESOLUÇÃO:

Retirando os dados importantes do problema:

• Polos: 6
• Frequência: 60 Hz
• Escorregamento s = 2,5% = 0,025
• Potência do entreferro = P_ag = 5000 W
• Perdas Mecânicas (atrito + ventilação) = P_mec = 312 W

Como queremos determinar o torque no eixo do motor, devemos primeiro encontrar a potência útil no eixo e velocidade mecânica real do motor.

Para Calcular a potência mecânica no eixo usamos a potência no entreferro (P_ag), pois ela se dividi em duas:

• Potência ôhmica do rotor (perdas no rotor) (P_r)
• Potência que é convertida em mecânica (P_conv)

Sabemos que:

Outra forma de encontrar o valor de P_conv é:

Para calcular a potência real dissipada no eixo do motor podemos utilizar a equação abaixo:

O próximo passo será calcular a velocidade real no eixo do rotor e para isso usaremos as seguintes formulas:

Velocidade síncrona:

Velocidade real no eixo com o escorregamento igual a 2,5%

Convertendo esse valor para rad / s

✅ Resposta Correta: Letra B.

QUESTÃO 21

Em uma instalação industrial, foi conectado um banco de capacitores com potência de 13,75 kVAr para compensação do fator de potência. Nessa situação, o fator de potência é de 0,96. Sendo a potência ativa total da instalação igual a 30 kW, qual era o fator de potência da instalação antes da conexão do banco de capacitores?

(A) 0,70
(B) 0,76
(C) 0,78
(D) 0,80
(E) 0,86

RESOLUÇÃO:

Dados do problema:

• Potência ativa total da instalação: P = 30 kW
• Potência reativa do banco de capacitores: Q_bc = 13,75 kVAr
• Após a conexão do banco de capacitores, o fator de potência vale:
  FP_novo = 0,96 

Pede-se:
O fator de potência antes da conexão do banco FP_antigo = ?

Inicialmente vamos calcular a nova potência reativa (Q_n) da instalação:

Agora vamos calcular a Potência Reativa antiga:

Usando propriedades trigonométricas temos que:

✅ Resposta Correta: Letra D.

QUESTÃO 22

O iluminamento (ou iluminância) é uma das grandezas utilizadas em projetos de luminotécnica. Admitindo A como a área da superfície em m2, L a luminância em cd/m2, F o fluxo luminoso em lm e P a potência consumida pela fonte luminosa em W, qual a expressão do iluminamento E e qual a simbologia de sua unidade no Sistema Internacional?

RESOLUÇÃO

1. O que é iluminância (E)?

A iluminância (também chamada de iluminamento) mede quanto fluxo luminoso (F) incide sobre uma área (A).

👉 Portanto, sua definição física é:

2. Unidades no Sistema Internacional

• Fluxo luminoso (F) → medido em lúmen (lm)
• Área (A) → medida em m²
• Iluminância (E) → logo será:

Então, lux (lx) é a unidade oficial da iluminância no SI.

🚫 O que a questão tenta confundir?

Ela introduz:

• L → luminância (cd/m²)
• F → fluxo luminoso (lm)
• P → potência consumida (W)

E coloca alternativas usando essas grandezas para confundir o candidato.

Mas a pergunta é clara:

qual a expressão do iluminamento admitindo A como área e F como fluxo luminoso?

Então basta usar a definição fundamental da iluminância.

✅ Resposta Correta: Letra A.

QUESTÃO 23

Um transformador monofásico de 100 kVA, 1.500/500 V, 60 Hz deve alimentar uma carga de 300 kVA com tensão nominal de 2.000 V. Para tal, realiza-se a conexão do transformador como autotransformador, alimentado pelo lado de alta tensão, que passa a ser o enrolamento comum à fonte de alimentação e à carga. Desconsidere as perdas do transformador.

Qual é a potência aparente transmitida à carga através dos enrolamentos de alta tensão e de baixa tensão e qual é a potência nominal do autotransformador, em kVA?

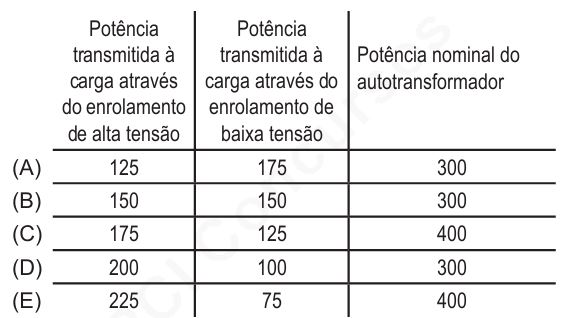
RESOLUÇÃO:

Dados do enunciado

• Transformador (isolado) de 100 kVA, tensões 1500 / 500 V (alta / baixa).
• Frequência irrelevante (60 Hz) — desprezamos perdas.
• Deseja alimentar uma carga de 300 kVA com tensão 2000 V.
• O transformador é ligado em autotransformador, alimentado pelo lado de alta tensão (1500 V); esse enrolamento de alta torna-se enrolamento comum entre fonte e carga.
• Note: 1500 V (fonte), 2000 V (carga) → o acréscimo necessário é 500 V, que corresponde ao enrolamento de baixa tensão do transformador (500 V). Ou seja: 1500 + 500 = 2000 V.

1) Corrente na carga

A corrente que circula na carga (reta) é

2) Potência aparente transmitida através do enrolamento de alta tensão

Esse enrolamento (1500 V) é o enrolamento comum (passa o valor de 1500 V × a corrente de carga):

3) Potência aparente transmitida através do enrolamento de baixa tensão

A diferença de tensão que o enrolamento de baixa fornece é 500 V, com a mesma corrente de carga (150 A):

(Verificação rápida: 225 + 75 = 300 kVA — corresponde à potência total da carga)

4) Potência nominal do autotransformador

Precisamos achar a capacidade nominal do autotransformador (em kVA). Use a relação entre a capacidade nominal do transformador isolado e a corrente no enrolamento isolado:

O transformador isolado é 100 kVA com a baixa tensão de 500 V → a corrente nominal naquele enrolamento (quando considerado como isolado) é

Quando o conjunto opera como autotransformador a corrente que o enrolamento isolado pode suportar é 200 A; a tensão total disponível pelo autotransformador é 2000 V (tensão da carga). Assim a potência aparente nominal do autotransformador é

(Interpretação: o enrolamento isolado de 100 kVA a 500 V, quando usado em autotransformador para fornecer 2000 V total, permite uma capacidade aparente global de 400 kVA.)

Resumo final (resposta)

• Potência transmitida a carga através do enrolamento de alta tensão: 225 kVA.
• Potência transmitida a carga através do enrolamento de baixa tensão: 75 kVA.
• Potência nominal do autotransformador: 400 kVA.

✅ Resposta Correta: Letra E.